Improving the GAN Part 2: Conditional and Controllable generation

Previously, I discussed in-depth the vanishing gradient problem in GANs and how it leads to unstable and ineffective learning. I then introduced the Wasserstein GAN, one of the popular solutions to this problem. While most research efforts into GANs have been in line with this goal of improving training stability, the game doesn’t end here. There are still so many aspects to image generation that can be explored, the three biggest ones being conditional generation, controllable generation, and high-resolution image synthesis. I’ll talk about conditional and controllable generation in this post.

What is Conditional Generation?

If I may describe the idea of generative modeling using the analogy of a vending machine, the basic GANs we have dealt with so far are like a simple gumball machine. You put your coin (which is like the latent noise vector) into the coin slot of the gumball machine (the GAN), and out comes a gumball that you can happily enjoy! But what if you want to have a red color gumball specifically? I’m sure you can see that this is not possible with our gumball machine, because after we put our coin in, what we get is a random gumball. This, in essence, is unconditional generation.

We need to upgrade our vending machine if we want it to dispense the item we want. To do this, instead of the simple gumball machine, we can consider a modern vending machine where you put in a coin (the noise vector), type the item code for the snack you want to dispense (known as the class encoding or class embedding), and voila, you get the snack you desired! This is conditional generation.

Creating this new vending machine, i.e., conditional GAN (CGAN) just requires some simple modifications. On the generator end, we have to modify the input to be the noise vector attached with the class encoding. A class encoding can be as simple as a one-hot vector – this is a vector that has a length equal to the number of classes, where the position of the n-th class is one, and the rest of the positions are zero. For example, if I have 3 classes: [Cat, dog, cow], the one-hot encoding of cat would be , for dog and for cow.

Modifications are made on the discriminator end as well. In the vanilla GAN, we just passed in a real and generated image, and the discriminator would classify it accordingly. But now, along with these images, we need to provide what class the image belongs to. For this, instead of a one-hot vector, we provide a one-hot tensor, basically a set of matrices where the n-th matrix for the n-th class contains ones, and the rest of the matrices contain zeros. The objective of the discriminator now changes: instead of “Does this image look real or fake?”, we are asking the discriminator, “Does this image of class X look real or fake?”.

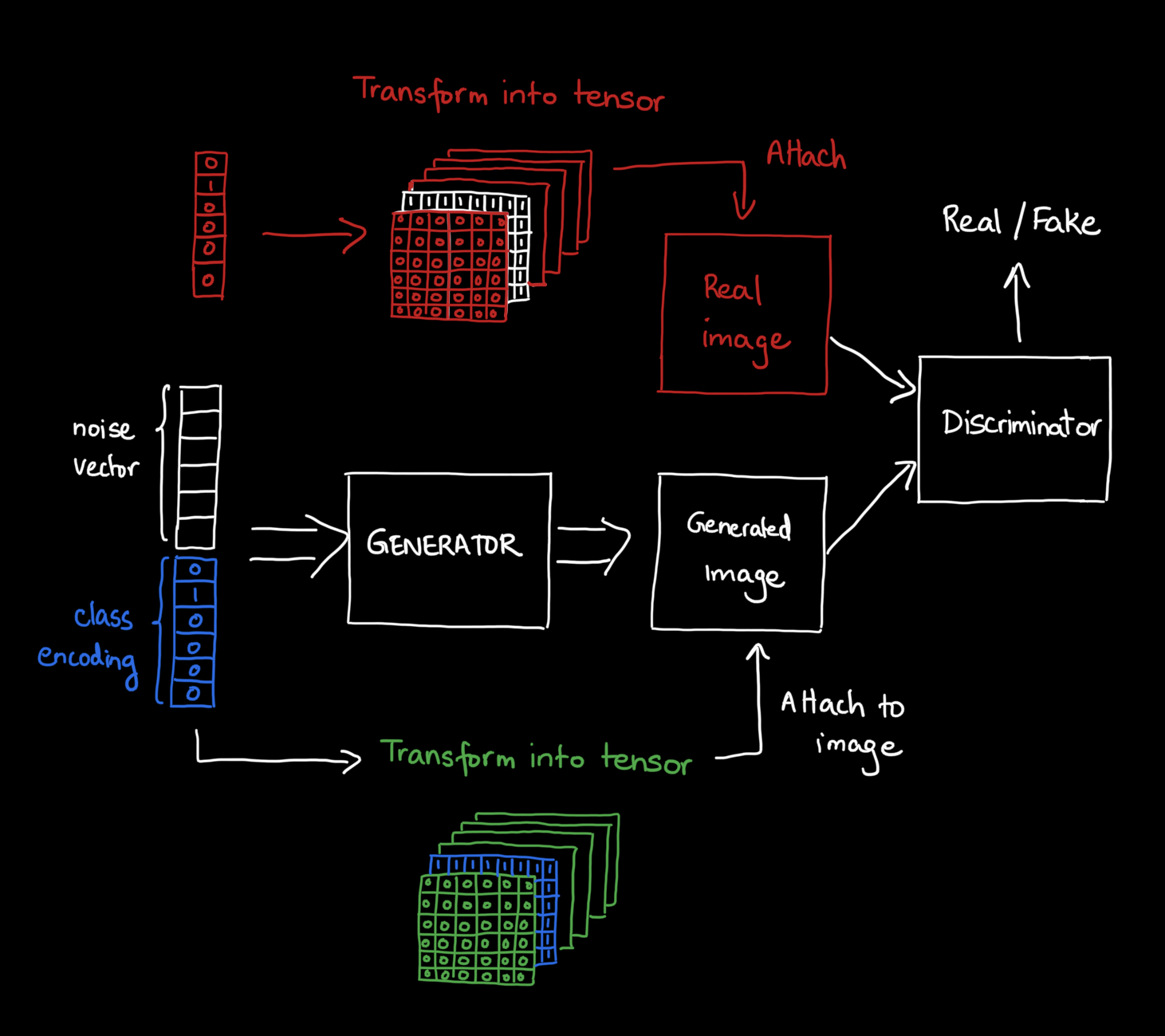
This naive and simple method of inputting one-hot vectors/tensors was proposed in the paper Conditional Generative Adversarial Networks by Mehdi Mirza and Simon Osindero. It isn’t the only way to communicate conditional information to a GAN, however. Other papers on conditional generation have used complex methods where class embeddings are injected inside the network at different points. For example, one study injected class info into the Batch Normalization layers of the deep network. Another study modified the discriminator to not only deal with an adversarial loss but also an auxiliary classification loss function, which forced the generated output to maximize a specific class probability. So, as you can see, there’s no one set way to do this task!

Controllable Generation: Navigating the Latent Space

Looking back on what we have learned so far, we started with a simple GAN that asks the question, “Can you generate a picture of an animal?”. Then in conditional GANs, we modified the setup to ask, “Can you generate a picture of a cat/dog/horse?”. Now, assuming that we have a well-trained and fully functional generative model that can synthesize an image of any class, we want to ask, “Can you generate a picture of a cat with white fur and green eyes?”. How can we do this custom image designing? This is where controllable generation comes in.

If we want to understand how to control a generated image, we need to understand the latent space of the GAN and how to navigate it. For example, in the diagram below, we have a latent vector that corresponds to an image of a girl with blue hair. If we imagine each component of this vector to correspond to some feature of the image, then modifying the vector component can change the resulting image.

Now it’s just a matter of figuring out how to modify the latent vector. One common approach is to gradually interpolate between different latent vectors along a direction and exploring how the image features change. But how do we find this direction? Well, we could leverage the power of existing deep learning classifiers. These classifiers are easier to train and are really good at detecting features. For example, suppose we want to modify the eye color of a person in the generated image. What we could do is first design a simple deep learning classifier for eye color. Then, using the feature information from this classifier, represented by the gradients, we can interpolate the latent vector along the gradient direction to change the generated eye color.

There is one big problem, though…

This all sounds really cool and straightforward to do, however, a major problem one can face with controllable generation is feature entanglement. This happens when there are not enough dimensions in the latent space to represent all the features of the image. The effect of this is that certain features can get entangled or grouped within the latent vector, such that modifying the latent vector in one feature can indirectly change another feature of the image. A simple example of this is the entanglement between hair length and gender. Suppose our GAN model has learned using a low-dimensional latent space; it will probably assume that all men have short hair while all women have long hair. So if my original latent vector generated a picture of a man and I modified it in the direction of hair length, the resulting image could be a woman instead.

A visualization of entanglement is shown below. Notice how, for example, modifying the “wavy hair” feature resulted in the man’s face morphing into a woman’s!

Ideally, we want a disentangled latent space where each feature is modeled independently. There are many ways this has been approached in the research literature, one example being the famous StyleGAN by NVIDIA, which applies a “mapping layer” onto the latent vector to create a disentangled representation.

That’s all!

To conclude, I would say conditional and controllable generation is where much of the fun in GANs research lies. In my next post in the “Improving the GAN” series, I’ll discuss the last major area of GANs research: high-resolution image synthesis. Until then, stay tuned!