I’m sure all of us, when learning something new, have had moments of inspiration where we’d think, “Oh wow! This idea makes sense and is so brilliant.” It’s these moments that I always look forward to, and what attracted me to machine learning was that I had these moments almost every day, only motivating me to keep learning more and more. When I think about my Aha moments, they are often the experiences where I encountered the simplest of ideas. One such concept is Bayes’ theorem, which forms the foundation for many more important ideas used in ML, data science, and statistics. Let’s explore what Bayes theorem is and why it’s so brilliant.
Taking a step back
To understand what Bayes theorem is, it’s important first to review basic probability, something I’m sure we’ve all studied in high school math. Probability is essentially a way of dealing with uncertain events. These events have some randomness associated with them and don’t follow a fixed process. Let’s look at the most common probability example: the coin toss. Let’s say I toss a coin; how likely is it to come up as heads? To calculate this, we divide the number of desired outcomes by the total number of possible outcomes. When I flip a coin, there are two possible outcomes – heads or tails. Our desired outcome is just that one where I get heads, so we say
is just a shorter way of saying “probability of heads.” So our probability of getting heads is 50% or 0.5. Will I get heads? I still don’t know. All I know is that there’s a 50% chance my coin will show heads. It’s also important to mention that any probability value will always be a number between 0 to 1(0% to 100%), with 0 meaning that the event will never occur and 1 meaning it will always occur.
Let’s look at another popular example: rolling a dice. Suppose I have a six-sided dice, what is the chance that I roll a 1? Simply using the formula above, its . To make it more interesting, what’s the chance that I get an even number? Well, there are three possibilities – I can roll a 2 or a 4 or a 6. For this we say
What even is probability?
Great, so using this probability formula, one can calculate a probability value for any basic scenario. But what does this concept mean? Most of us in high school (at least me!) just saw probability as another math formula you plug and play. After seeing its applications in data science and machine learning, I better understood what probability means and why it is relevant to life.
Looking back to the early research by mathematicians and philosophers, there have been many different probability interpretations. The probability formula I showed previously is called the “classical interpretation” of probability, which is the first rigorous effort to formalize this idea. Another popular interpretation is the “frequentist interpretation,” which states that a probable event occurs frequently. So, if I now look at the coin toss from a frequentist point of view, the way I would calculate the is to measure the frequency of heads when flipping a coin multiple times:
In this case, if I flip the coin just 5-10 times, I may not get the same 0.5 probability as in the classical definition. For example, if I do five experiments where I see two heads and three tails, then the frequency of heads is . Only as I do more and more experiments (suppose 100 or 1000 experiments), my calculated frequency will get closer and closer to the probability value of 0.5. You can try this yourself and see that it works!
Another interpretation of probability is the BAYESIAN interpretation. This interpretation arises from the ideology that we, as humans, like to have initial beliefs or opinions about something. Only through experiences and collecting more information do we update this belief. Here, the belief is synonymous with probability. For example, I believe that Pizza Hut makes the best pizza ever, so I say that is roughly 0.99 or 99%. Now suppose I have a bad day and the pizza turns out to be horrible, then I update my belief about Pizza Hut so that now
is roughly 0.89 or 89%. If my next experience turns out great again, I update this belief, and the probability can go up. But how does one update this belief or probability? Enters Bayes theorem.
Bayes Theorem
Bayes theorem is a straightforward formula for updating beliefs. A related idea to this theorem is that of “conditional” probability. Recall a normal probability asks the question, “What is the chance that X occurs?”. Conditional probability asks the question “What is the chance that X occurs, given that we know Y occurs?” which is conventionally represented by . The | followed by “Y occurs” is just a shorthand way of saying “given that Y occurs.” The way we calculate this conditional probability is using the formula:
This equation probably doesn’t make sense at first sight so let’s do a simple example.
The Pizza Party
Suppose I’m hosting a party for my 100 friends and I need to decide what food to order. I know that some of my friends are vegetarians while some are non-vegetarian. I also know that some like pizza, and some hate pizza. I sent a survey to all my friends to collect this information, and I’ve summarized the results into a nice little table below.
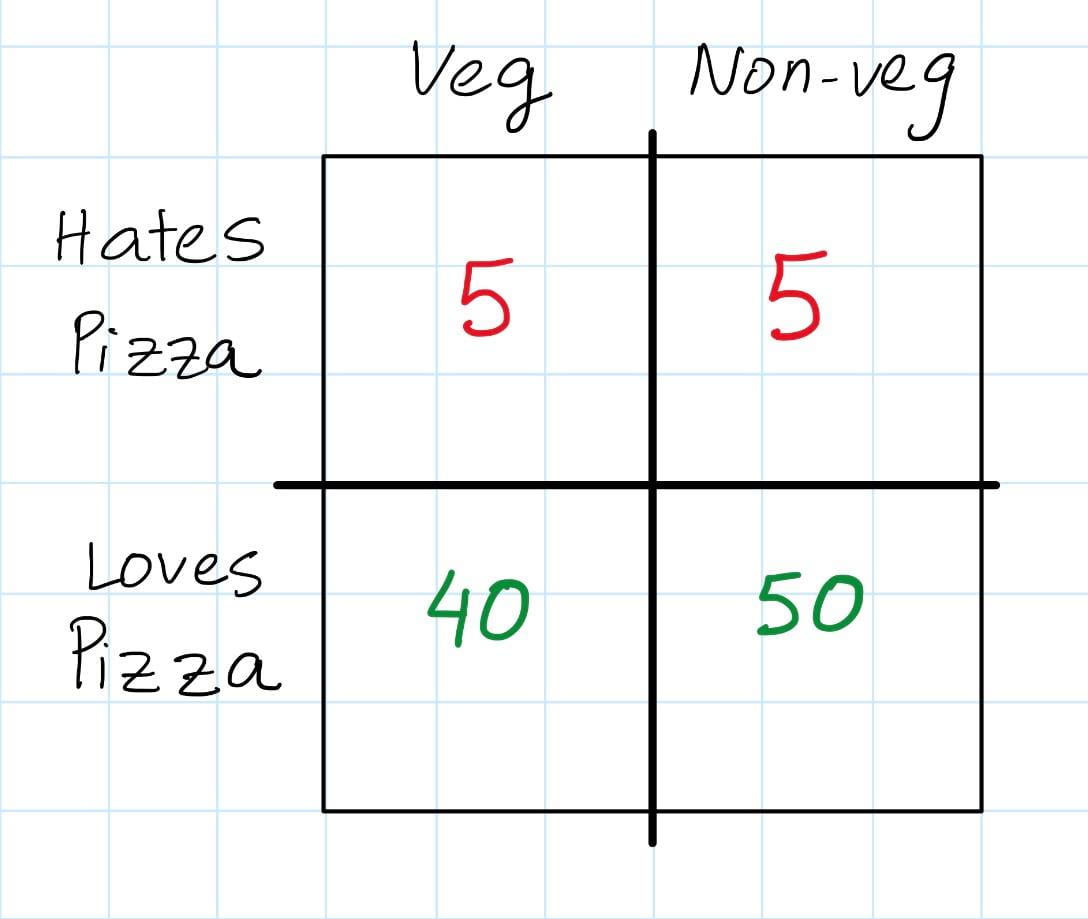
As a warm-up, what’s the probability someone loves pizza? It’s just
Great stuff! Now, here comes a slightly trickier problem: what is the probability that someone loves pizza, given that they are a vegetarian or ?
The way I think about this is that if I’ve been given information that the person is a vegetarian, then I can focus on the group of vegetarian people and ignore the non-vegetarians. Instead of focusing on all my 100 friends, I’m focusing on just my 45 vegetarian friends. Now, in my vegetarian friend group, what is the probability that someone loves pizza? Simple, it’s just . If I express this as a mathematical formula, I get
As you can see, this is the same as the conditional probability formula where Y = “Vegetarian” and X = “Loves pizza”. To reiterate, by dividing by , I’m focusing on just the vegetarian friend group. The numerator is just the number of people who love pizza AND are vegetarian (also called the joint probability).
Now to bring the concept home and connect it to the bigger picture, let’s do one last interesting problem. Suppose I was in a different scenario – I got information that the person loves pizza, and I want to know the probability that this person is a vegetarian. So now instead of , I’m calculating
. It’s important to realize that these two are not the same! The information I’m getting in each is different. In the former, I have got information that the person is vegetarian, so I focused only on the vegetarians’ group. In the latter, I got information that the person loves pizza, so now I’m focusing on the group of people who all love pizza. If I write this mathematically, the conditional probability equation for this new scenario is
[Equation 1]
Compare this equation to the equation from the previous problem:
[Equation 2]
Now we can do something interesting here. While both equations calculate a different conditional probability, both have the same numerator, which is P(Loves Pizza and Vegetarian). If I do some basic algebra on [Equation 1], I’ll find that
I can plug this back into [Equation 2] to get that
and Ta-Da! This is the Bayes Theorem for my pizza party example.
You’re probably super confused right now or wondering why on earth I did this tedious math. Well, let me summarize the above ugly equations into something neater:
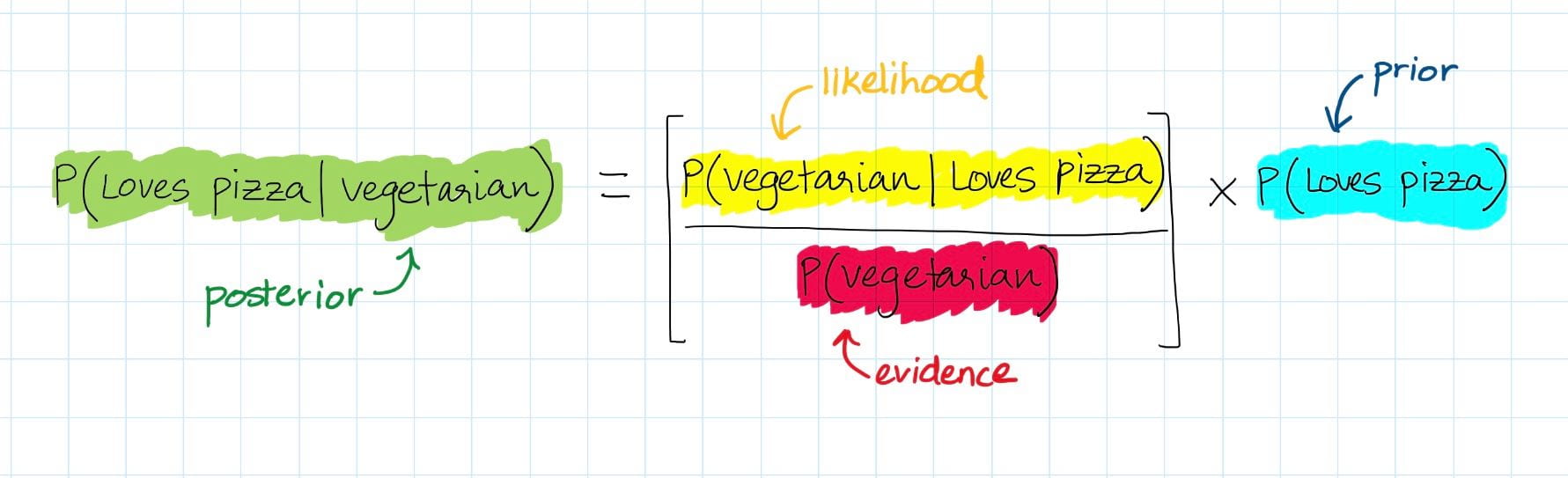
On the right side of the equation, we have the probability of someone loving pizza, , called the prior (because it’s the probability BEFORE seeing evidence). This is multiplied with some fraction
to get
, which is called the posterior (because it’s the probability AFTER seeing evidence). The details about this fraction are slightly harder to explain, but for now, understand that it just has two parts – a likelihood, which is the numerator, and the evidence, which is the denominator.
Why is this equation cool? Because recall that originally, we calculated that is 0.90. In other words, if I pick some random person out from my party, there’s a 90% chance that this person loves pizza. But then, I found that
. So after getting the extra information or evidence that the person is a vegetarian, the probability of him/her loving pizza decreased to 89% from 90%. This result makes sense because if you look at the table, more non-vegetarians love pizza compared to vegetarians. Putting it short, we had a belief about how much someone loves pizza, then we got some extra information about the person, and finally, we updated our belief about how much he loves pizza. This is what Bayesian thinking is all about!
Conditional probability, Bayes theorem, and Bayesian inference are fundamental concepts in machine learning. Bayesian thinking is valuable because it allows us to factor previous knowledge into our beliefs, allowing us to model dynamic scenarios and generate useful insights from data. In future posts, I hope to delve more in detail into the different applications of these concepts.
One thought on “Bayes Theorem – A primer”